Some corrections to a problem result in lengthy, ongoing discussions. On Brilliant.org, my original correction still raises the question "are we missing yet more 'smart' answers?"
The Original Question
"Which of the following regular polygons can be folded into a pyramid without cutting or overlapping any area?"
When I pointed out that the answer is both the triangle (resulting in a regular tetrahedron) and the square (resulting in an irregular pyramid of positive volume), it changed the game. The question had to be rewritten, and those who had earlier answered "square" were granted credit.
Definitions
Still, even the revised question is awkwardly worded. I can now prove that any regular polygon can be folded into a regular tetrahedron, "without cutting or overlapping," so long as excess flaps are permitted to hang external to the pyramid. This would not be so had the original question made a requirement that it form "only just a regular pyramid, and nothing more."
Definitions would also help if pyramid and "regular pyramid" were more clearly defined. I think the common definition of a "regular pyramid" is one whose base is any regular polygon, but whose side faces are all isosceles triangles of an arbitrary but equal height.
There do exist trivial solutions for square and hexagon if the pyramid needn't have a positive height and thus positive volume. A smaller square inscribed inside a larger square (from the midpoints of the sides of the larger) can form a base for a square pyramid of zero height. Similarly, a smaller triangle can be inscribed inside a larger hexagon, its verteces attached to every other vertex of the hexagon. When these are folded in, the sum angle of the two flaps are equal to the angle of the base polygon, so no height results. It is unclear if this breaks the questions definition of "overlapping," since there is no excess area in the process: They may "lap" but not "overlap," depending on the definitions.
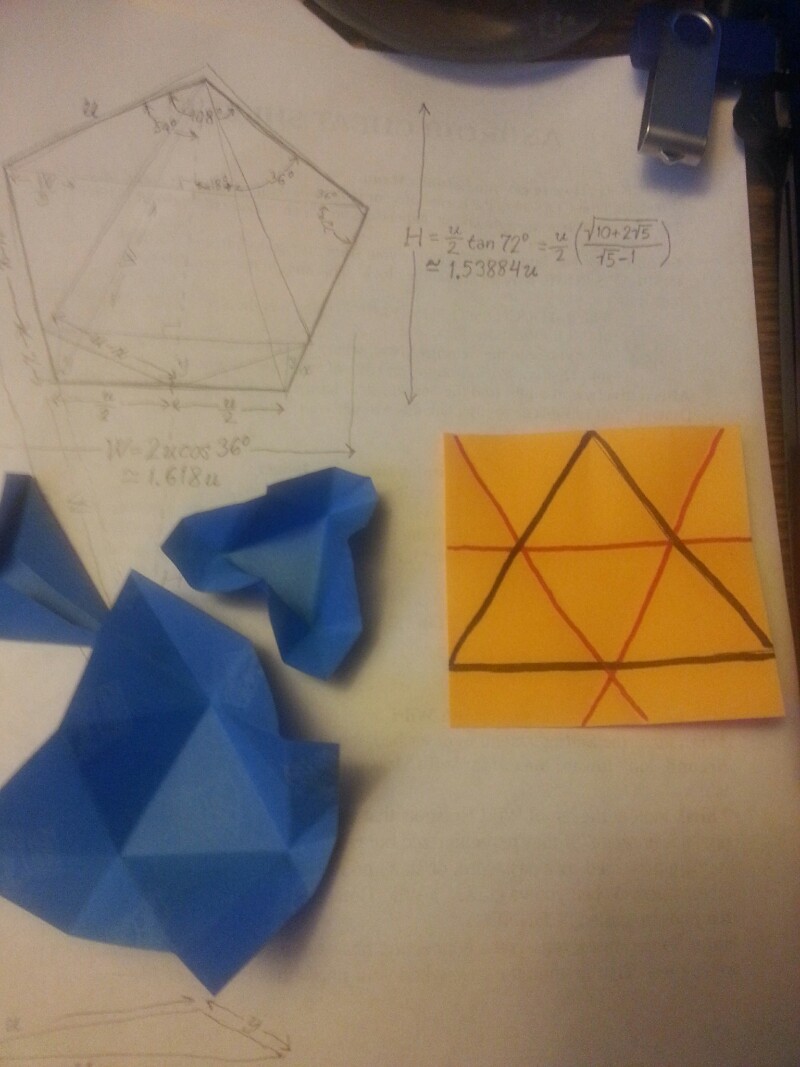
Proof any regular polygon can be folded into a regular tetrahedron
Lemma 1: A regular triangle can be inscribed into any regular polygon
Pick your regular polygon and select one of its sides. The polygon is regular, so an axis of symmetry can be drawn down its center from the midpoint of the selected side. By placing the vertex of the inscribed triangle onto this midpoint, it is seen that it abuts the inside and outside of the polygon, yet resides in neither. The same is true of the other vertices of the inscribed triangle: They are constructed against whichever side of the polygon they intersect when following a 30 degree angle left or right of the axis of symmetry.
Construction
Let us inscribe the triangle in black, as depicted in the attached photo of a triangle inside an orange square. Let us then draw red lines through the midpoints of the inscribed triangle. The black lines of the base will be folded back/outward, and the red lines will be folded up/inward. Since the inscribed triangle's vertices abut the larger polygon's outer edges, there is no exterior excess along the axis of symmetry drawn through any of the base's vertices. These three vertices will meet as the pinnacle of the pyramid above the base. And because the red folds are angled to create incomplete regular tetrahedrons of their own, they fold away from the central tetrahedron without needing to be cut or overlapped. \(\tag*{q.e.d. \(\Box\)}\)
Conclusion
If the question were reworded to require just a pyramid and nothing more nor less, then the only solution would be the regular triangle. But if flaps are welcome as presented here, then any regular polygon can provide this solution. The only "wasteless" pyramid is the pyramid itself: nothing less, nothing more.
